/* Petit programme qui calcul numériquement une intégrale selon l'algorithme de Simpson.
Avant de l'executer, il faut entrer:
- l'expression de la fonction f: ligne 12;
- les bornes inférieure a et supérieure b de l'intégrale: lignes 39 et 40;
- le nombre de mesures n (n est entier!!!): ligne 41.
------------------------------------------------------------------------------------------------------ */
class Fonction{ //Classe fonction: definit fonction et Simpson
double f (double x) { //DEFINIR la fonction à intégrer.
return Math.Cos(x);
}
double IntSimpson(double a, double b,int n){ //Methode de Simpson pour calcul intégrale
int i,z; //a= borne inférieure et b, borne supérieure d'intégration
double h,s; //n = nombre de pas
n=n+n;
s = f(a)*f(b);
h = (b-a)/n;
z = 4;
for(i = 1; i<n; i++){
s = s + z * f(a+i*h);
z = 6 - z;
}
return (s * h)/3;
}
}
class integration{ //Class resultat: calcul l'integrale et affiche le resultat.
public static void main(String args[]){
Fonction fonction; //Appel class fonction
fonction = new Fonction();
double a = ???? ; //RENTRER les valeurs souhaitées de a, b et n !!!
double b = ???? ;
int n = ???? ;
double resultat = fonction.IntSimpson(a,b,n); //Applique méthode simpson à fonction
System.out.println("Integrale vaut: " + resultat); //Affiche les résultats
}
}
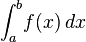
qué buscáis un (número aproximado) numérica o simbólica (una fórmula que representa el resultado exactamente) solución? – meriton
Para la integración simbólica es posible que desee considerar http://integrals.wolfram.com/index.jsp –
@meriton Este hilo tiene alguna solución para la aproximación numérica. ¿Pero cómo obtengo la solución simbólica? –