Muestra uniformemente al azar de una unidad simple de n dimensiones

Question

muestreo de manera uniforme al azar de una unidad de n-dimensional simplex es la forma elegante de decir que desea n números aleatorios tal que

• son todas libres negativo,
• suman a uno, y
• cada posible vector de n números no negativos que sumen a uno son igualmente probables.

En el caso n = 2, quiere muestrear uniformemente del segmento de la línea x + y = 1 (es decir, y = 1-x) que está en el cuadrante positivo. En el n = 3 caso de que esté muestreo de la parte en forma de triángulo del plano x + y + z = 1 que está en el octante positivo de R3:

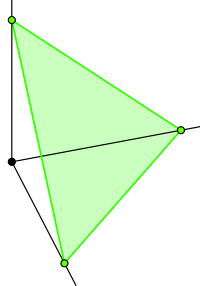
(Imagen de http://en.wikipedia.org/wiki/Simplex.)

Tenga en cuenta que elegir n números aleatorios uniformes y luego normalizarlos para que sumen a uno no funciona. Terminas con un sesgo hacia números menos extremos.

Del mismo modo, elegir n-1 números aleatorios uniformes y luego tomar la enésima para ser uno menos la suma de ellos también introduce un sesgo.

Wikipedia ofrece dos algoritmos para hacer esto correctamente: http://en.wikipedia.org/wiki/Simplex#Random_sampling (Aunque el segundo momento, sólo afirma que es correcta en la práctica, no en la teoría que espero que limpiar eso o aclarar que cuando entiendo esto mejor.. Inicialmente metí en un "ADVERTENCIA: documento de tal y tal afirma que lo siguiente es incorrecto" en esa página de Wikipedia y otra persona lo convirtió en la advertencia "funciona solo en la práctica")

Finalmente, la pregunta: ¿Cuál considera que es la mejor implementación del muestreo símplex en Mathematica (preferiblemente con confirmación empírica de que es correcto)?

preguntas relacionadas

• Generating a probability distribution
• java random percentages

Answer 1

este código puede trabajar:

samples[n_] := Differences[Join[{0}, Sort[RandomReal[Range[0, 1], n - 1]], {1}]] 

Básicamente que acaba de elegir n - 1 lugares en el intervalo de [0,1] a dividirlo luego tomar el tamaño de cada una de las piezas utilizando Differences.

Una ejecución rápida de Timing muestra que es un poco más rápido que la primera respuesta de Janus.

Answer 2

Después de un poco de excavar alrededor, he encontrado this page que da una buena aplicación de la distribución de Dirichlet. A partir de ahí, parece que sería bastante simple seguir el método de Wikipedia 1. Esta parece ser la mejor manera de hacerlo.

Como prueba:

In[14]:= RandomReal[DirichletDistribution[{1,1}],WorkingPrecision->25] 
Out[14]= {0.8428995243540368880268079,0.1571004756459631119731921} 
In[15]:= Total[%] 
Out[15]= 1.000000000000000000000000 

Una parcela de 100 muestras:

alt text http://www.public.iastate.edu/~zdavkeos/simplex-sample.png

Answer 3

estoy con zdav: la distribución de Dirichlet parece ser la forma más fácil por delante, y el algoritmo para muestrear la distribución de Dirichlet a la que se refiere zdav también se presenta en la página de Wikipedia en el Dirichlet distribution.

Implementada, es un poco exagerado realizar la distribución completa de Dirichlet primero, ya que todo lo que realmente necesita es n muestras aleatorias Gamma[1,1]. Comparar a continuación
simple aplicación

SimplexSample[n_, opts:OptionsPattern[RandomReal]] := 
    (#/Total[#])& @ RandomReal[GammaDistribution[1,1],n,opts] 

aplicación de Dirichlet completa

DirichletDistribution/:Random`DistributionVector[ 
DirichletDistribution[alpha_?(VectorQ[#,Positive]&)],n_Integer,prec_?Positive]:= 
    Block[{gammas}, gammas = 
     Map[RandomReal[GammaDistribution[#,1],n,WorkingPrecision->prec]&,alpha]; 
     Transpose[gammas]/Total[gammas]] 

SimplexSample2[n_, opts:OptionsPattern[RandomReal]] := 
    (#/Total[#])& @ RandomReal[DirichletDistribution[ConstantArray[1,{n}]],opts] 

sincronización

Timing[Table[SimplexSample[10,WorkingPrecision-> 20],{10000}];] 
Timing[Table[SimplexSample2[10,WorkingPrecision-> 20],{10000}];] 
Out[159]= {1.30249,Null} 
Out[160]= {3.52216,Null} 

Así que el total de Dirichlet es un factor de 3 más lento. Si necesita m> 1 punto de muestra a la vez, probablemente pueda ganar más haciendo (#/Total[#]&)/@RandomReal[GammaDistribution[1,1],{m,n}].

Answer 4

Aquí es una buena aplicación concisa del segundo algoritmo de Wikipedia:

SimplexSample[n_] := Rest@# - Most@# &[Sort@Join[{0,1}, RandomReal[{0,1}, n-1]]] 

Eso es una adaptación de aquí: http://www.mofeel.net/1164-comp-soft-sys-math-mathematica/14968.aspx (Originalmente tenían Unión en lugar de ordenar @ Ingreso - este último es un poco más rápido.)

(Véanse los comentarios de algunas pruebas de que esto es correcto!)

Answer 5

He creado un algoritmo para la generación aleatoria uniforme sobre un simplex. Puede encontrar los detalles en el documento en el siguiente enlace: http://www.tandfonline.com/doi/abs/10.1080/03610918.2010.551012#.U5q7inJdVNY

hablar brevemente, puede utilizar las siguientes fórmulas de recursión para encontrar los puntos al azar sobre el n-dimensional simplex:

x = 1- R^1/n-1

x _k = (1- Σ _{i = 1} ^k x _i) (1- R _k^1/nk), k = 2, ..., N-1

x _n = 1- Σ _{i = 1}^n-1 x _i

Dónde R_I'S están número aleatorio entre 0 y 1.

Ahora estoy tratando de hacer un algoritmo para generar muestras aleatorias uniformes de constrained simplex.that es la intersección entre un simplex y un cuerpo convexo.