Hasta ahora parece que la ecuación de base 2 de Fabrice Bellard es el camino a seguirComputing π a "infinito" precisión binaria en C#
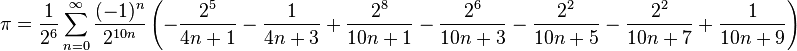
Irónicamente esto requerirá un tipo BigReal; ¿tenemos esto para .Net? .Net 4.0 tiene BigInteger.
¿Alguien tiene una versión de Haskell?
Puesto que usted está pidiendo una versión Haskell, here is a paper de Jerzy Karczmarczuk, llamado "La técnica más fiable en el mundo para calcular π":
Este documento es un exercice atípico en codificación funcional perezoso , escrito para diversión e instrucción. Se puede leer y ser entendido por cualquiera que entiende el lenguaje de programación Haskell. Mostramos cómo implementar la fórmula Bailey-Borwein-Ploue para π de una manera co-recursiva, incremental que produce los dígitos 3, 1, 4, 1, 5, 9.. . hasta la memoria agotamiento. Esta no es una forma de proceder si alguien necesita muchos dígitos ! Nuestra estrategia de codificación es perversa y peligrosa, y se destruye de manera demostrable. Se basa en la aritmética sobre el dominio de secuencias infinitas de dígitos que representa las fracciones propias expandidas en una base entera. Mostramos cómo manipular : agregar, multiplicar por un número entero , etc. tales secuencias de a la izquierda ad infinitum, que obviamente no pueden funcionar en todos los casos debido a ambigüedades. Algunas consecuencias filosóficas profundas son discutidas en las conclusiones.
Realmente no resuelve el problema de una manera eficiente o muy práctica, pero es entretenida y muestra algunos de los problemas con la aritmética de precisión infinita perezosa.
Luego está también this paper by Jeremy Gibbons.
¡Muchas gracias! ¡Este es exactamente el tipo de cosas que estaba buscando! –
Wikipedia detalla muchas maneras de obtener aproximaciones numéricas de pi here. También dan algún ejemplo de pseudo-código
Editar: Si está interesado en este tipo de problemas matemáticos sin tener ningún problema relacionado del mundo real para resolver (que definitivamente es una buena actitud para tener, en mi humilde opinión), podría visite el Euler Project page
Lo siento, has leído mal mi pregunta. No busco nada dentro del rango de tipos nativos. Quiero el verdadero "BigNum" π. –
Tampoco busco una solución "horneada", solo sugerencias/ideas genuinas sobre esto. No pensé que era la única persona en Stackoverflow que estaba interesada en este tipo de cosas en mi tiempo libre. –
@Bent. Este es un problema matemático clásico. Está cubierto ampliamente en la página de wikipedia que publiqué, y honestamente dudo que obtengas algunas ideas nuevas aquí. ¿Qué estás buscando exactamente? – Brann
Existe tal posibilidad de procesar grandes números racionales en DLR-idiomas dinámicos (por ejemplo, IronPython). O puede usar cualquier implementación portátil de C/C++ de grandes números reales a través del P/Invoke.
de lejos mi grifo favorita Haskell para PI proviene de Jeremy Gibbons:
pi = g(1,0,1,1,3,3) where
g(q,r,t,k,n,l) =
if 4*q+r-t<n*t
then n : g(10*q,10*(r-n*t),t,k,div(10*(3*q+r))t-10*n,l)
else g(q*k,(2*q+r)*l,t*l,k+1,div(q*(7*k+2)+r*l)(t*l),l+2)
La formación matemática que justifica que la aplicación se puede encontrar en:
¡Impresionante! Gracias por la referencia! –
Cuál es su motivo ? :) – zproxy
No estoy seguro si esto le interesa: http://pebblesteps.com/post/Calculating-PI-using-the-Monte-Carlo-method-using-F.aspx – Benjol
"¿Cuál es su motivo? :) - zproxy " - ulterior –