Cálculo de la k-core de un gráfico por vértices iterativamente la poda es bastante fácil. Sin embargo, para mi aplicación, me gustaría poder agregar vértices al gráfico inicial y obtener el núcleo actualizado sin tener que volver a calcular todo el k-core desde cero. ¿Existe un algoritmo confiable que pueda aprovechar el trabajo realizado en iteraciones anteriores?incrementales algoritmo k-core
Para los curiosos, la k-núcleo está siendo utilizado como una etapa de preprocesamiento en un algoritmo de descubrimiento clique. Se garantiza que cualquier grupo de tamaño 5 formará parte de los 4 núcleos de un gráfico. En mi conjunto de datos, el 4-core es mucho más pequeño que todo el gráfico, por lo que puede forzarlo desde allí. Incrementar la adición de vértices permite que el algoritmo funcione con un conjunto de datos lo más pequeño posible. Mi conjunto de vértices es infinito y está ordenado (números primos), pero solo me importa la camarilla con el número más bajo.
Editar:
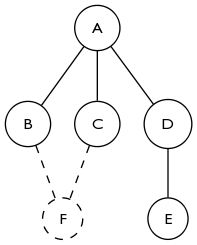
Pensando en ello un poco más basado en la respuesta de akappa, la detección de la creación de un bucle es de hecho crítico. En el siguiente gráfico, el núcleo 2 está vacío antes de agregar F. Agregar F no cambia el grado de A, pero agrega A a 2 núcleos. Es fácil extender esto para ver cómo el cierre de un bucle de cualquier tamaño haría que todos los vértices se unieran simultáneamente a los 2 núcleos.
Adición de un vértice puede tener un efecto sobre la coreness vértices de una distancia arbitraria de distancia, pero quizás esto es centrarse demasiado el comportamiento en el peor de los casos.